|
Section
04 Part 05 – Bit shifting |
|
“A shift is necessary toward lifestyles less geared to environmental damaging consumption patterns.” ~Maurice Strong |
Introduction
These
next set of instructions I’m about to show you are very similar; they all deal
with what is known as “bit shifting”.
To
explain the shifting process, we’ll use d0 as an example and make it contain
0000004C. We’ll take the byte 4C on the
end, and look at it in bits:
|
0100 1100 |
When
shifting the bits, there are two directions, left and right. So if we shifted the byte 4C left by 1 bit,
we would get:
|
< 1001 1000 < |
You
can see the 0’s and 1’s have moved over 1 bit to the left. If we shifted 4C right by 1 instead, we would
get:
|
> 0010 0110 > |
The
0’s and 1’s have moved over 1 bit to the right.
This is the standard idea of “bit shifting”.
Logical and
Arithmetic shifting
When shifting
bits to the left or right, an empty space is opened up, for example:
|
1100 1100 |
When
shifting right by 1 bit, we get:
|
> ?110 0110 > |
As
the bits were shifted, the space on the far left (marked as ?) has appeared. The question is; is it filled with 0, or
1? This is decided by
“logical”/“arithmetic”.
When
using logical shifting, the answer is
always 0:
|
> 0110 0110
> |
When
using arithmetic shifting, the answer is
decided by the MSB (most significant bit).
So, let’s just look at the byte before
it was shifted:
|
1100 1100 |
As
you can see, the MSB is 1. After an
arithmetic shift:
|
> 1110 0110 > |
The
MSB stays as 1. If the bit were 0 on the
other hand:
|
0100 1100 |
After
an arithmetic shift:
|
> 0010 0110 > |
The
MSB stays as 0.
Here’s
a graphical example of a logical shift “right”:
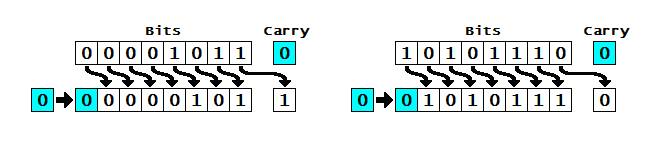
Here’s
a graphical example of an arithmetic shift “right”:
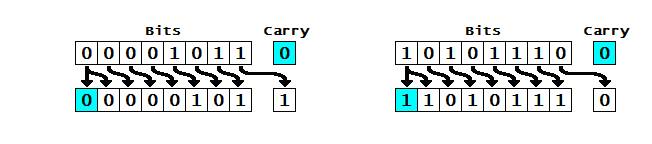
For
shifting “left” however, both logical shifting and arithmetic shifting have the same result, the LSB (least significant bit) always changes to 0:
|
1111 1111 |
After
a logical or arithmetic shift left:
|
< 1111 1110 < |
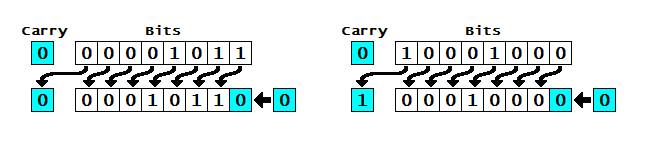
The
result is always 0 no matter what the LSB was.